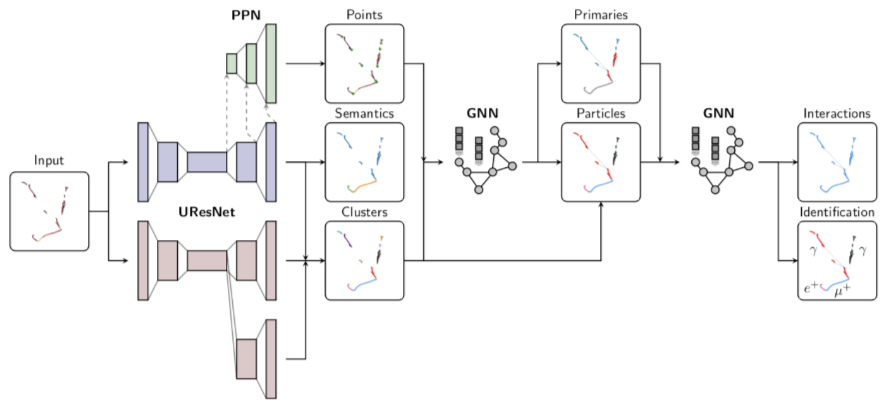
Introduction to lartpc_mlreco3d Analysis Tools¶
This notebook is a tutorial on how to use trained models in lartpc_mlreco3d for high level physics analysis, including but not limited to event selection. The purpose of this tutorial is to make inference and physics analysis using neural network models of lartpc_mlreco3d more accessible to non-experts and to make the process of asking simple questions (ex. how many particles in given image?) independent from knowing implementation details of separate sub-modules (which may include specific settings on hyperparameters and post-processing scripts). The tutorial is designed as follows:
Overview of
lartpc_mlreco3d.analysis(analysis helper functions and classes)ParticleandInteractionData StructuresHow to use
FullChainEvaluatorExample usage of
FullChainEvaluatorand how to run inference and save information viaanalysis/run.py.
Please send questions and any bug reports to the #lartpc-mlreco3d channel on SBN Slack workspace.
1. Overview of lartpc_mlreco3d.analysis¶
The ML full chain (lartpc_mlreco3d/mlreco/models/full_chain.py) is a combination of multiple (convolutional and graphical) neural networks, chained together to build information from the bottom-up direction while extracting useful features on each level of detail. However, in many cases the level of detail provided by both the full chain code and its output is too excessive for asking simple high-level questions, such as:
How many interactions are there in this image?
How many leptons does this interaction contain?
What is the five-particle classification accuracy for this model?
What is the signal (however one defines it) selection efficiency/purity?
Although it is possible to answer these questions using the output dictionary of the full chain, the pathway to that often involves asking people around how to set hyperparameters, how to call some specific post-processing functions, what convention to use when selecting viable particle/interaction candidates, etc.
The lartpc_mlreco3d analysis tools are designed to organize full chain output information into more human-friendly format and provide an common and convenient user interface to perform high level analysis without requiring explicit knowledge of the full chain submodules. The tools are stored under lartpc_mlreco3d/analysis, which is outside of all neural-network related works in lartpc_mlreco3d/mlreco (on purpose). The practical usage of the analysis code will be much more transparent through demonstration using the full chain.
NOTE: Please use the latest develop branch from the main repository DeepLearningPhysics/lartpc_mlreco3d/develop. We will first load the full chain model to this notebook:
import numpy as np
import plotly
import pandas as pd
import matplotlib.pyplot as plt
import seaborn
from pprint import pprint
import seaborn as sns
sns.set(rc={
'figure.figsize':(20, 10),
})
sns.set_context('talk') # or paper
import plotly.graph_objs as go
from plotly.subplots import make_subplots
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
init_notebook_mode(connected=False)
import os, sys
SOFTWARE_DIR = '%s/lartpc_mlreco3d' % os.environ.get('HOME') # Path to your `lartpc_mlreco3d`
DATA_DIR = os.environ.get('DATA_DIR')
# Set software directory
sys.path.append(SOFTWARE_DIR)
import torch
print(torch.cuda.is_available())
from mlreco.main_funcs import process_config, prepare
import yaml
True
/usr/local/lib/python3.8/dist-packages/MinkowskiEngine/__init__.py:36: UserWarning:
The environment variable `OMP_NUM_THREADS` not set. MinkowskiEngine will automatically set `OMP_NUM_THREADS=16`. If you want to set `OMP_NUM_THREADS` manually, please export it on the command line before running a python script. e.g. `export OMP_NUM_THREADS=12; python your_program.py`. It is recommended to set it below 24.
We will use the ICARUS dataset coupled with its latest weight. The following cell loads the full chain configuration file as a dictionary (cfg) and builds the full chain neural network model:
cfg = yaml.load(open('%s/inference.cfg' % DATA_DIR, 'r').read().replace('DATA_DIR', DATA_DIR),Loader=yaml.Loader)
# pre-process configuration (checks + certain non-specified default settings)
process_config(cfg, verbose=False)
# prepare function configures necessary "handlers"
hs = prepare(cfg)
dataset = hs.data_io_iter
Config processed at: Linux ampt017 3.10.0-1160.42.2.el7.x86_64 #1 SMP Tue Sep 7 14:49:57 UTC 2021 x86_64 x86_64 x86_64 GNU/Linux
$CUDA_VISIBLE_DEVICES="0"
Welcome to JupyROOT 6.22/09
Loading file: /sdf/home/l/ldomine/lartpc_mlreco3d_tutorials/book/data/mpvmpr_062022_test_small.root
Loading tree sparse3d_reco
Loading tree sparse3d_reco_chi2
Loading tree sparse3d_reco_hit_charge0
Loading tree sparse3d_reco_hit_charge1
Loading tree sparse3d_reco_hit_charge2
Loading tree sparse3d_reco_hit_key0
Loading tree sparse3d_reco_hit_key1
Loading tree sparse3d_reco_hit_key2
Loading tree sparse3d_pcluster_semantics_ghost
Loading tree cluster3d_pcluster
Loading tree particle_pcluster
Loading tree particle_mpv
Loading tree sparse3d_pcluster_semantics
Loading tree sparse3d_pcluster
Loading tree particle_corrected
Found 101 events in file(s)
Warning in <TClass::Init>: no dictionary for class larcv::EventNeutrino is available
Warning in <TClass::Init>: no dictionary for class larcv::NeutrinoSet is available
Warning in <TClass::Init>: no dictionary for class larcv::Neutrino is available
Shower GNN: True
Track GNN: True
Particle GNN: False
Interaction GNN: True
Kinematics GNN: False
Cosmic GNN: False
Since one of the GNNs are turned on, process_fragments is turned ON.
Fragment processing is turned ON. When training CNN models from
scratch, we recommend turning fragment processing OFF as without
reliable segmentation and/or cnn clustering outputs this could take
prohibitively large training iterations.
Shower GNN: True
Track GNN: True
Particle GNN: False
Interaction GNN: True
Kinematics GNN: False
Cosmic GNN: False
Since one of the GNNs are turned on, process_fragments is turned ON.
Fragment processing is turned ON. When training CNN models from
scratch, we recommend turning fragment processing OFF as without
reliable segmentation and/or cnn clustering outputs this could take
prohibitively large training iterations.
Freezing 82 weights for a sub-module ppn
Freezing 141 weights for a sub-module uresnet_lonely
Freezing 141 weights for a sub-module uresnet_deghost
Freezing 146 weights for a sub-module graph_spice
Freezing 120 weights for a sub-module grappa_track
Freezing 120 weights for a sub-module grappa_shower
Restoring weights for from /sdf/home/l/ldomine/lartpc_mlreco3d_tutorials/book/data/weights_full_mpvmpr_062022.ckpt...
Done.
Now that the full chain and its trained weights are loaded into the notebook, let’s do a single forward pass and inspect the results.
data_blob, res = hs.trainer.forward(dataset)
Deghosting Accuracy: 0.9830
Segmentation Accuracy: 0.9900
PPN Accuracy: 0.8843
Clustering Accuracy: 0.2691
Clustering Edge Accuracy: 0.1252
Shower fragment clustering accuracy: 0.9581
Shower primary prediction accuracy: 0.9434
Track fragment clustering accuracy: 0.9937
Interaction grouping accuracy: 0.9763
Particle ID accuracy: 0.8409
Primary particle score accuracy: 0.9755
print("Number of fieldnames in full chain output dictionary: {}".format(len(res.keys())))
Number of fieldnames in full chain output dictionary: 120
We first introduce the FullChainEvaluator, which is an user-interface wrapper class for lartpc_mlreco3d/analysis.
from analysis.classes.ui import FullChainEvaluator
To configure an instance of FullChainEvaluator, we need the following parameters.
data_blob(dict of lists): dictionary containing lists ofnp.ndarrays, with list length equal to the batch size (unwrapped)res(dict): output dictionary from full chain model (unwrapped)cfg(dict): inference.cfgconfiguration file. Mainly for setting batch size, dataset path, output log file path, etc.deghosting(bool, optional): whether the full chain of interest supports deghosting. This option is mostly reserved for development, and for most circumstances it will most certainly be set toTrue.
By unwrapped, we mean that in the inference configuration file, the unwrapper option should be set to True:
trainval:
seed: 123
unwrapper: unwrap_3d_mink
predictor = FullChainEvaluator(data_blob, res, cfg, deghosting=True) # Only run this cell once! This is due to deghosting being an in-place operation.
We can check how many images are in this batch:
print(predictor)
FullChainEvaluator(num_images=10)
2. Obtaining True and Predicted Labels for Visualization¶
Here we plot the predicted and true labels for semantic, fragment, group, and interaction predictions side-by-side using Plotly. The plotted labels are set to group labels (particle instance labels) by default, but you are free to plot other labels provided in the following cell.
entry = 0 # Specify the batch_id
pred_seg = predictor.get_predicted_label(entry, 'segment') # Get predicted semantic labels from batch id <entry>
true_seg = predictor.get_true_label(entry, 'segment') # Get true semantic labels from batch id <entry>
pred_fragment = predictor.get_predicted_label(entry, 'fragment')
true_fragment = predictor.get_true_label(entry, 'fragment')
pred_group = predictor.get_predicted_label(entry, 'group')
true_group = predictor.get_true_label(entry, 'group')
pred_interaction = predictor.get_predicted_label(entry, 'interaction')
true_interaction = predictor.get_true_label(entry, 'interaction')
pred_pids = predictor.get_predicted_label(entry, 'pdg')
true_pids = predictor.get_true_label(entry, 'pdg')
pred_plot, true_plot = pred_group, true_group
Here, the full chain code and the evaluator predictor is handling all hyperparameters and post-processing necessary to properly produce the predicted and true labels. This should allow one to inspect the full chain output at different levels of detail for better understanding of when and how the reconstruction succeeds/fails.
Some boilerplate for better plotly formatting:
from mlreco.visualization import scatter_points, scatter_cubes, plotly_layout3d
from mlreco.utils.metrics import unique_label
layout = plotly_layout3d()
bg_color = 'rgba(0,0,0,0)'
grid_color = 'rgba(220,220,220,100)'
layout = dict(showlegend=False,
autosize=True,
height=1000,
width=1000,
margin=dict(r=20, l=20, b=20, t=20),
plot_bgcolor='rgba(255,255,255,0)',
paper_bgcolor='rgba(255,255,255,0)',
scene1=dict(xaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
yaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
zaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
aspectmode='cube'),
scene2=dict(xaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
yaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
zaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
aspectmode='cube'),
scene3=dict(xaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
yaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
zaxis=dict(dict(backgroundcolor=bg_color, gridcolor=grid_color)),
aspectmode='cube'))
Prediction is shown in left, while true labels are shown in right.
make_plots = True
if make_plots:
fig = make_subplots(rows=1, cols=2,
specs=[[{'type': 'scatter3d'}, {'type': 'scatter3d'}]],
subplot_titles=('Prediction', 'Truth'),
horizontal_spacing=0.05, vertical_spacing=0.04)
fig.add_trace(go.Scatter3d(x=data_blob['cluster_label'][entry][:,1],
y=data_blob['cluster_label'][entry][:,2],
z=data_blob['cluster_label'][entry][:,3],
mode='markers',
marker=dict(
size=2,
color=pred_plot,
# cmax=4, cmin=-1,
colorscale="rainbow",
reversescale=True,
opacity=1
),
hovertext=pred_plot,
name='Prediction Labels'
), row=1, col=1)
fig.add_trace(go.Scatter3d(x=data_blob['cluster_label'][entry][:,1],
y=data_blob['cluster_label'][entry][:,2],
z=data_blob['cluster_label'][entry][:,3],
mode='markers',
marker=dict(
size=2,
color=true_plot,
# cmax=4, cmin=-1,
colorscale="rainbow",
reversescale=True,
opacity=1
),
hovertext=true_plot,
name='Prediction Labels'
), row=1, col=2)
fig.layout = layout
fig.update_layout(showlegend=True,
legend=dict(xanchor="left"),
autosize=True,
height=1000,
width=2000,
margin=dict(r=20, l=20, b=20, t=20))
fig.update_layout(
scene1 = dict(
xaxis = dict(range=[0,768],),
yaxis = dict(range=[0,768],),
zaxis = dict(range=[0,768],),),
scene2 = dict(
xaxis = dict(range=[0,768],),
yaxis = dict(range=[0,768],),
zaxis = dict(range=[0,768],),),
margin=dict(r=20, l=10, b=10, t=10))
iplot(fig)
3. Particle and Interaction Data Structures¶
When performing event selection analysis, it is often convenient to organize information into units of particles and interactions:
A
Particleis a set of voxels that share the same predicted group id.A
TruthParticleis a set of voxels that share the same true group id.An
Interactionis a set of voxels that share the same predicted interaction id.A
TruthInteractionis a set of voxels that share the same true interaction id.
As such, Particle and Interaction are predicted quantities reconstructed from the ML chain, while their “true” counterparts are quantities defined using true labels. Although the two classes share many of their properties, we deliberately decide to separate any truth information from interfering with predicted quantities.
Let’s process the current image’s ML reco output information into these data structures. The get_particles function will organize the point cloud of a selected batch id (entry) into a list of Particle instances. The only_primaries=True option will only select particles that originate from a vertex:
predicted_particles = predictor.get_particles(0, only_primaries=False)
predicted_particles = predictor.get_particles(0, only_primaries=True)
pprint(predicted_particles)
[Particle( Image ID=0 | Particle ID=4 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 99.93% | Interaction ID: 9 | Size: 307 ),
Particle( Image ID=0 | Particle ID=5 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 91.16% | Interaction ID: 9 | Size: 100 ),
Particle( Image ID=0 | Particle ID=10 | Semantic_type: Track | PID: Pion | Primary: 1 | Score = 94.35% | Interaction ID: 9 | Size: 248 ),
Particle( Image ID=0 | Particle ID=13 | Semantic_type: Track | PID: Proton | Primary: 1 | Score = 99.83% | Interaction ID: 9 | Size: 243 ),
Particle( Image ID=0 | Particle ID=14 | Semantic_type: Track | PID: Muon | Primary: 1 | Score = 99.86% | Interaction ID: 9 | Size: 997 )]
Here, the Score refers to the softmax probability value of the most confident prediction. For example, in the above cell, the full chain predicts with 99.93% softmax probability that the particle with Particle ID=4 is of class Photon. The Size refers to the total number of voxels with the given ID (the voxel count of the particle).
The counterpart for true particles is the function get_true_particles:
true_particles = predictor.get_true_particles(0)
pprint(true_particles)
[TruthParticle( Image ID=0 | Particle ID=0 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 4 | Size: 997 ),
TruthParticle( Image ID=0 | Particle ID=1 | Semantic_type: Track | PID: Proton | Primary: 1 | Interaction ID: 4 | Size: 250 ),
TruthParticle( Image ID=0 | Particle ID=2 | Semantic_type: Track | PID: Pion | Primary: 1 | Interaction ID: 4 | Size: 276 ),
TruthParticle( Image ID=0 | Particle ID=3 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Interaction ID: 4 | Size: 323 ),
TruthParticle( Image ID=0 | Particle ID=4 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Interaction ID: 4 | Size: 111 ),
TruthParticle( Image ID=0 | Particle ID=14 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 5 | Size: 1561 ),
TruthParticle( Image ID=0 | Particle ID=15 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 12 | Size: 2212 ),
TruthParticle( Image ID=0 | Particle ID=16 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 7 | Size: 1100 ),
TruthParticle( Image ID=0 | Particle ID=17 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 13 | Size: 155 ),
TruthParticle( Image ID=0 | Particle ID=18 | Semantic_type: Shower Fragment | PID: Electron | Primary: 1 | Interaction ID: 3 | Size: 307 ),
TruthParticle( Image ID=0 | Particle ID=19 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 1 | Size: 2205 ),
TruthParticle( Image ID=0 | Particle ID=20 | Semantic_type: Shower Fragment | PID: Electron | Primary: 1 | Interaction ID: 11 | Size: 206 ),
TruthParticle( Image ID=0 | Particle ID=21 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 8 | Size: 108 ),
TruthParticle( Image ID=0 | Particle ID=22 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 2 | Size: 1512 ),
TruthParticle( Image ID=0 | Particle ID=23 | Semantic_type: Shower Fragment | PID: Electron | Primary: 1 | Interaction ID: 6 | Size: 274 ),
TruthParticle( Image ID=0 | Particle ID=24 | Semantic_type: Shower Fragment | PID: Electron | Primary: 1 | Interaction ID: 9 | Size: 295 ),
TruthParticle( Image ID=0 | Particle ID=25 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 10 | Size: 1246 )]
Note that TruthParticle does not contain the Score value, and currently it does not differ between MPV (multi-particle vertex) and MPR (multi-particle rain). This means that if prediction was to be perfect (particle clustering perfectly matches that of truth labels) and only_primaries was set to True, the MPR particles will be omitted from the predicted list of particles while remaining in the list of true particles.
Similarly, for interactions we have:
predicted_interactions = predictor.get_interactions(entry, drop_nonprimary_particles=True)
pprint(predicted_interactions)
[Interaction 9, Valid: True, Vertex: x=390.70, y=234.45, z=2367.98
--------------------------------------------------------------------
- Particle 4: PID = Photon, Size = 307, Match = []
- Particle 5: PID = Photon, Size = 100, Match = []
- Particle 10: PID = Pion, Size = 248, Match = []
- Particle 13: PID = Proton, Size = 243, Match = []
- Particle 14: PID = Muon, Size = 997, Match = []
]
Here, we see that Interaction 9 has 5 particles with particle IDs [5, 4, 10, 13, 14] (not to be confused with PDG codes, the particle IDs are nominal integer values used to separate distinct instances), with a vertex located at \(\vec{v}\) = (390.70, 234.45, 2367.98). When performing get_interactions, the algorithm first retrives all particles in the given entry using get_particles, groups the particles into separate Interaction classes, and then runs a post-processing script specifically reserved for vertex prediction.
Each entry in predicted_interactions has data type Interaction. For example, you can retrive the list of particles contained in this interactions is List[Particle]:
ia_0 = predicted_interactions[0]
pprint(ia_0.particles)
[Particle( Image ID=0 | Particle ID=4 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 99.93% | Interaction ID: 9 | Size: 307 ),
Particle( Image ID=0 | Particle ID=5 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 91.16% | Interaction ID: 9 | Size: 100 ),
Particle( Image ID=0 | Particle ID=10 | Semantic_type: Track | PID: Pion | Primary: 1 | Score = 94.35% | Interaction ID: 9 | Size: 248 ),
Particle( Image ID=0 | Particle ID=13 | Semantic_type: Track | PID: Proton | Primary: 1 | Score = 99.83% | Interaction ID: 9 | Size: 243 ),
Particle( Image ID=0 | Particle ID=14 | Semantic_type: Track | PID: Muon | Primary: 1 | Score = 99.86% | Interaction ID: 9 | Size: 997 )]
It is also straightforward to get true particles:
predicted_interactions = predictor.get_true_interactions(entry, drop_nonprimary_particles=True)
pprint(predicted_interactions)
[TruthInteraction 4, Vertex: x=391.35, y=235.02, z=2367.80
-----------------------------------------------
- Particle 0: PID = Muon, Size = 997, Match = []
- Particle 1: PID = Proton, Size = 250, Match = []
- Particle 2: PID = Pion, Size = 276, Match = []
- Particle 3: PID = Photon, Size = 323, Match = []
- Particle 4: PID = Photon, Size = 111, Match = []
,
TruthInteraction 5, Vertex: x=509.23, y=410.47, z=2733.18
-----------------------------------------------
- Particle 14: PID = Muon, Size = 1561, Match = []
,
TruthInteraction 12, Vertex: x=916.69, y=191.20, z=673.99
-----------------------------------------------
- Particle 15: PID = Muon, Size = 2212, Match = []
,
TruthInteraction 7, Vertex: x=667.93, y=900.68, z=2656.70
-----------------------------------------------
- Particle 16: PID = Muon, Size = 1100, Match = []
,
TruthInteraction 13, Vertex: x=940.22, y=766.15, z=4440.70
-----------------------------------------------
- Particle 17: PID = Muon, Size = 155, Match = []
,
TruthInteraction 3, Vertex: x=387.22, y=232.95, z=2107.00
-----------------------------------------------
- Particle 18: PID = Electron, Size = 307, Match = []
,
TruthInteraction 1, Vertex: x=341.08, y=607.49, z=990.26
-----------------------------------------------
- Particle 19: PID = Muon, Size = 2205, Match = []
,
TruthInteraction 11, Vertex: x=776.40, y=676.65, z=3546.51
-----------------------------------------------
- Particle 20: PID = Electron, Size = 206, Match = []
,
TruthInteraction 8, Vertex: x=692.11, y=912.95, z=3105.85
-----------------------------------------------
- Particle 21: PID = Muon, Size = 108, Match = []
,
TruthInteraction 2, Vertex: x=386.29, y=375.94, z=5593.15
-----------------------------------------------
- Particle 22: PID = Muon, Size = 1512, Match = []
,
TruthInteraction 6, Vertex: x=640.28, y=967.47, z=2288.28
-----------------------------------------------
- Particle 23: PID = Electron, Size = 274, Match = []
,
TruthInteraction 9, Vertex: x=759.73, y=467.38, z=2236.87
-----------------------------------------------
- Particle 24: PID = Electron, Size = 295, Match = []
,
TruthInteraction 10, Vertex: x=764.55, y=820.51, z=3056.33
-----------------------------------------------
- Particle 25: PID = Muon, Size = 1246, Match = []
]
More information could be read from the docstrings of Particle/TruthParticle and Interaction/TruthInteraction here.
4. Matching particles and interactions¶
To evaluate the performance of the full chain, we require a matching procedure that relates predicted Particles/Interactions with the most appropriate TruthParticles/TruthInteractions. Several issues arise when doing this:
One can either start with the set of predictions and match a corresponding true particle for each predicted entity (
pred -> truematching), or vice versa (true -> predmatching). The result will in general be different.For a
pred -> truematching scheme, it is possible for two or more predicted particles to map to the same true particle (the most obvious example happens when a single true particle is fragmented into separate predictions, due to mistakes in clustering).For a
pred -> truematching scheme, it is possible for a given predicted particle to have no match whatsoever (ex. a fake particle is created due to mistakes in deghosting, or a particle not associated with an interaction is mistakenly assigned an interaction vertex).
The above points hold similarly for the reverse case (true -> pred).
The matching algorithms for particles and interactions are implemented in match_particles and match_interactions member functions:
matched_particles = predictor.match_particles(entry, only_primaries=True, mode='pred_to_true')
pprint(matched_particles)
[(Particle( Image ID=0 | Particle ID=4 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 99.93% | Interaction ID: 9 | Size: 307 ),
TruthParticle( Image ID=0 | Particle ID=3 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Interaction ID: 4 | Size: 323 )),
(Particle( Image ID=0 | Particle ID=5 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Score = 91.16% | Interaction ID: 9 | Size: 100 ),
TruthParticle( Image ID=0 | Particle ID=4 | Semantic_type: Shower Fragment | PID: Photon | Primary: 1 | Interaction ID: 4 | Size: 111 )),
(Particle( Image ID=0 | Particle ID=10 | Semantic_type: Track | PID: Pion | Primary: 1 | Score = 94.35% | Interaction ID: 9 | Size: 248 ),
TruthParticle( Image ID=0 | Particle ID=2 | Semantic_type: Track | PID: Pion | Primary: 1 | Interaction ID: 4 | Size: 276 )),
(Particle( Image ID=0 | Particle ID=13 | Semantic_type: Track | PID: Proton | Primary: 1 | Score = 99.83% | Interaction ID: 9 | Size: 243 ),
TruthParticle( Image ID=0 | Particle ID=1 | Semantic_type: Track | PID: Proton | Primary: 1 | Interaction ID: 4 | Size: 250 )),
(Particle( Image ID=0 | Particle ID=14 | Semantic_type: Track | PID: Muon | Primary: 1 | Score = 99.86% | Interaction ID: 9 | Size: 997 ),
TruthParticle( Image ID=0 | Particle ID=0 | Semantic_type: Track | PID: Muon | Primary: 1 | Interaction ID: 4 | Size: 997 ))]
Here, matched_particles will be a list of (Particle, TruthParticle) tuples (in Python typing notation–List[Tuple[Particle, TruthParticle]]). We can see that particles with similar sizes are matched together.
Note: if a true particle match does not exist for a given prediction, the method will place a
Noneinstead of assigning anyTruthParticleinstance (as could be seen above).The
mode='pred_to_true'refers to the matching conventionpred -> true. Fortrue -> predmatching, we simply replace it asmode='true_to_pred'.
The match_particles method does not take into account interaction grouping information to match particles. That is, regardless of interaction grouping it will work with predicted and true particles of a given image, and work out the best possible matching configuration for the two sets.
If one desires to match particles hierarchically, proceeding from matching interactions and then particles within those interactinos, match_interactions(entry, match_particles=True) is the correct method:
matched_interactions = predictor.match_interactions(entry) # Default mode is match_particles=True
matched_interactions
[(Interaction 9, Valid: True, Vertex: x=390.70, y=234.45, z=2367.98
--------------------------------------------------------------------
- Particle 4: PID = Photon, Size = 307, Match = [3]
- Particle 5: PID = Photon, Size = 100, Match = [4]
- Particle 10: PID = Pion, Size = 248, Match = [2]
- Particle 13: PID = Proton, Size = 243, Match = [1]
- Particle 14: PID = Muon, Size = 997, Match = [0] ,
TruthInteraction 4, Vertex: x=391.35, y=235.02, z=2367.80
-----------------------------------------------
- Particle 0: PID = Muon, Size = 997, Match = [14]
- Particle 1: PID = Proton, Size = 250, Match = [13]
- Particle 2: PID = Pion, Size = 276, Match = [10]
- Particle 3: PID = Photon, Size = 323, Match = [4]
- Particle 4: PID = Photon, Size = 111, Match = [5] )]
Now we see that the Match = [...] string is filled with the matched particle ID values. More precisely, we read the above result as follows: Particle 4 inside Interaction 9 is matched with TruthParticle 3 inside TruthInteraction 4.
Note that TruthParticle can have multiple matches, meaning the (predicted) matched particles all have the maximum overlap with the same TruthParticle.
5. Example: Evaluating full chain five-particle classification performance using lartpc_mlreco3d/analysis.¶
Let’s say you want to produce a confusion matrix to evaluate five-particle classification performance on the full chain, using the icarus ghost-inclusive dataset. You first start by defining a selection algorithm under analysis/algorithms/selection.py. Let’s call the algorithm name “five_particle_classification”. The decorator function under analysis.decorator is designed to handle most of the common boilerplate code such as importing the config file, initializing the Trainval class, iterating the dataset for a given number of iterations, and saving the results to a csv file (many of the code was borrowed from the same design principle used in mlreco/post_processing). The specific details of your analysis script (in this case, saving particle type information) is independent from this boilerplate. So let’s define a function five_particle_classification which will match interactions, match particles, and retrive predicted and true particle type information, which we intend to save as a csv file.
from collections import OrderedDict
from analysis.classes.ui import FullChainEvaluator
from analysis.decorator import evaluate
from analysis.classes.particle import match
@evaluate(['result_pt.csv', 'result_tp.csv'], mode='per_batch')
def five_particle_classification(data_blob, res, data_idx, analysis_cfg, module_config):
pred_to_truth, truth_to_pred = [], []
return [pred_to_truth, truth_to_pred]
The first argument of the evaluate decorator is a list of strings indicating the names of the output csv files. Here, I want to save my results on two separate files, one for pred -> true matching (result_pt.csv) and another for true -> pred matching (result_tp.csv). The outputs pred_to_truth and truth_to_pred are each list of dictionaries, where each dictionary represents a single row in the output csv file, with keys indicating the column headers.
A. General form of the evaluation function.¶
As one can observe from the above example, an evaluation function takes the following form:
@evaluate([filename_1, filename_2, ..., filename_n], mode=MODE_STRING)
def eval_func(data_blob, res, data_idx, analysis_cfg, cfg):
...
return [output_1, output_2, ..., output_n]
Every evaluation function eval_func should have five input parameters as shown above, and must be accompanied with the @evaluate decorator. Here, data_blob and res are in exactly the same format as we used before in this notebook: the former refers to the input data dictionary while the latter refers to the output dictionary from the full chain. The parameter data_idx is a capture variable from the evaluate decorator, indicating the batch id number of a given image when running the eval_func on per single image mode. For the purpose of this tutorial we can ignore this. The important parameters are the following:
analysis_cfg: configuration dictionary for running analysis jobs.cfg: the config file for the full chain, as was used when initializingFullChainEvaluator.
This is best understood with an example: since we defined the function five_particle_classification under analysis/algorithms/selection.py, we make a file analysis.cfg:
analysis.cfg¶
analysis:
name: five_particle_classification
...
We know that the FullChainEvaluator must run under the deghosting mode turned on, which is a parameter for the FullChainEvaluator. So we define that in the analysis.cfg file:
analysis.cfg¶
analysis:
name: five_particle_classification
deghosting: True
...
B. Defining fieldnames and default values.¶
For the csv logger to work consistently, we must specify the name of the columns and the default values for each of the columns, in case an unmatched particle or interaction pair occurs. These go under the name fields. We also specify the output log directory in which the output csv file will be stored.
The decorator also has an option mode='per_batch', which means that the five_particle_classification function will be executed for a given batch rather than on a single image. This means that data_blob will contain BATCH_NUMBER units of data, which we can iterate over to access single images. The choice mode='per_batch' is mostly a matter of convenience, as FullChainEvaluator can already handle batches as we seen before.
@evaluate(['result_pt.csv', 'result_tp.csv'], mode='per_batch')
def five_particle_classification(data_blob, res, data_idx, analysis_cfg, module_config):
# Set default fieldnames and values. (Needed for logger to work)
fields = OrderedDict(analysis_cfg['analysis']['fields'])
pred_to_truth, truth_to_pred = [], []
deghosting = analysis_cfg['analysis']['deghosting']
pred_to_truth, truth_to_pred = [], []
return [pred_to_truth, truth_to_pred]
analysis.cfg¶
analysis:
name: five_particle_classification
processor_cfg:
spatial_size: 768
log_dir: ./logs/icarus
iteration: 400
deghosting: True
fields:
index: -1
pred_particle_type: -1
true_particle_type: -1
...
Here we’ve placed nominal values of -1 for default particle types.
@evaluate(['result_pt.csv', 'result_tp.csv'], mode='per_batch')
def five_particle_classification(data_blob, res, data_idx, analysis_cfg, module_config):
# Set default fieldnames and values. (Needed for logger to work)
fields = OrderedDict(analysis_cfg['analysis']['fields'])
pred_to_truth, truth_to_pred = [], []
deghosting = analysis_cfg['analysis']['deghosting']
predictor = FullChainEvaluator(data_blob, res, cfg, analysis_cfg, deghosting=deghosting)
image_idxs = data_blob['index']
# 1. Get Pred -> True matching (for each predicted particle, match one of truth)
for i, index in enumerate(image_idxs):
matches = predictor.match_interactions(i, mode='pt', match_particles=True)
for interaction_pair in matches:
pred_int, true_int = interaction_pair[0], interaction_pair[1]
if true_int is not None:
pred_particles, true_particles = pred_int.particles, true_int.particles
else:
pred_particles, true_particles = pred_int.particles, []
matched_particles, _, _ = match(pred_particles, true_particles,
primaries=True, min_overlap_count=1)
for ppair in matched_particles:
update_dict = OrderedDict(fields) # Initialize the csv row update dictionary
update_dict['index'] = index # In case we want to save image numbers for mistakes analysis.
if ppair[1] is not None: # Check for unmatched pairs (particle, None)
update_dict.update(
{
'pred_particle_type': ppair[0].pid, # pid means particle type
'true_particle_type': ppair[1].pid
}
)
pred_to_truth.append(update_dict)
...
# (do the same with true -> pred)
return [pred_to_truth, truth_to_pred]
Once this is done, you call analysis/run.py from the terminal as follows:
$ python3 $PATH_TO_LARTPC_MLRECO3D/analysis/run.py $PATH_TO_CFG $PATH_TO_ANALYSIS_CFG